機器學習可行嗎?

最根本的現實是機器學習即便挑選的演算法以及假說設定的再好, 最終也只能代表 inside Data 能有不錯的表現, 關於 outside Data 的一切我們都是未知, 接下來就是探討對於現實我們是否能增加一些假設條件, 來對於這些未知的結果得到較為可靠的預測 (透過數學的工具)。

Topic I (Hoeffding's Inequality)

Sample (取樣) 的代表性, 假設取樣中某特徵呈現的機率為 ν, 而實際機率為 μ, 則兩者存在以下不等式的關係稱 Hoeffding's Inequality

P [|ν - μ| > ɛ] ≤ 2 exp (-2ɛ²N), ɛ 為誤差範圍、N 為取樣數

• 誤差愈大 或 取樣數愈大, 不等式右項就愈小, 表示發生的可能性愈低
• ν = μ 是 PAC (Probably Approximately Correct) 很大的機會是對的, 但還是有例外

Topic II

將 Hoeffding's Inequality 導入 Learning Model 推敲 outside Data 的準確性, 這邊有個前提是假設產生 訓練資料(inside D) 及 測試資料(outside D) 存在相同的 P 機率分佈。

P [|E_in(h) - E_out(h)| > ɛ] ≤ 2 exp (-2ɛ²N)

所以當取樣 (N) 夠多時

• E_in(h) ≈ E_out(h)
• 又當 E_in(h) 夠小時, g = f is PAC (Probably Approximately Correct)
• 此評估 outside D 的方式, 說明了如何驗證單一一個 Hypothesis 的好壞, 但不保證此 Hypothesis 在挑選過程中會被 Algorithm 挑選到

Topic III (Pick Hypothesis Algorithm)

再來討論 Algorithm 挑選 Hypothesis 的限制, E_in(h) 最低不一定代表是最佳, 因為 sample 到不好的資料會讓 E_in(h)、E_out(h) 相距很遠, 當有選擇時, 會讓選出錯誤的 Hypothesis 機率增加 (更容易選到 overfitting 的假說, 只要某個 h 挑選到 bad sample data 時, 會以為它是如此的完美, 但實際上對 outside D 的預測意義並不大)。

那究竟這個遇見 bad Sample 的機率有多高呢?

$$\begin{aligned} \ & \mathbb{P}_{\mathcal{D}}[BAD\ \mathcal{D}] \\\ \ & = \mathbb{P}_{\mathcal{D}}[BAD\ \mathcal{D}\ for\ h_1\ or\ BAD\ \mathcal{D}\ for\ h_2\ or\ ...\ or\ BAD\ \mathcal{D}\ for\ h_M]\\\ \ & \leq \mathbb{P}_{\mathcal{D}}[BAD\ \mathcal{D}\ for\ h_1] + \mathbb{P}_{\mathcal{D}}[BAD\ \mathcal{D}\ for\ h_2]+...+\mathbb{P}_{\mathcal{D}}[BAD\ \mathcal{D}\ for\ h_M] (union \ \ bound)\\\ \ & \leq 2exp(-2\epsilon ^2N) + \leq 2exp(-2\epsilon ^2N) + ... + \leq 2exp(-2\epsilon ^2N) \\\ \ & = 2Mexp(-2\epsilon ^2N) \end{aligned}$$

令存在有限 M 種的 Hypothesis時, 由 Topic I Hoeffding's Inequality 知道個別 Hypothesis 選中不好的資料 (E_in(h)、E_out(h) 相距很遠) 的機率不高, 所以 Σ _(i=0~M) P_D[BAD of D]≤ 2 M exp (-2ɛ²N), 可得知當

• 取樣個數夠多時
• 存在有限個數 M 的 Hypothesis

E_in(g) ≈ E_out(g) is PAC 一樣會成立。

Ｍ 的挑選是個取捨, 過小的話可以讓選中不好的 g 機會降低, 但是可以選的選項太少反而不一定存在可以挑出夠小的 E_in(h), 太大的 M 則是讓選出不好的 g 機率增加。

Topic IV 收斂 Hypothesis Set

延續上一個 Topic, ∞ 多個 Hypothesis 會讓 Topic III 不等式的 Upper Bound 沒有意義, 原因在於 Set 之中其實存在許多相似重疊的 Hypothesis, 它們造成挑選到錯誤機率的疊加效果過於放大 (使得 bound 太寬鬆), 接著我們要收斂 Set 裡的個數, 首先嘗試對 Hypothesis 做分類, 方法是從 Data 的角度看待這些 Hypothesis 是將其歸類為何。

Effective Number of Lines 定義為將 output 劃分不同種類的可能性 (≤ 2^N), 透過分類後 Hypothesis 之後可得到

$\mathbb{P}[|E_{in}(g)-E_{out}(g)|\gt \epsilon]\leq 2\cdot effective(N)\cdot exp(-2\epsilon^2N)$

ex. 2D Perceptron, binary classification output y = {+1, -1}。

• 僅一筆資料時, 存在兩種 分割線 (多維度時是高維平面) 將其 output 分為 +1 或 -1

• 二筆資料時, 存在四種 分割線 (多維度時是高維平面) 將這兩個資料特徵向量 output 分為 +1 或 -1

• 三筆資料時, 最多存在八種 分割線 (多維度時是高維平面), 但如果三點共線時則僅六種 (+1,-1,+1), (-1,+1,-1) 的 分割線／高維平面 不存在

• 四筆資料時, 則最多只有 14 種 (對角線為相同 output 的分割線不存在)

• 五筆資料時, 則最多只有 22 種 (將所有點排在一個圓上, 將相鄰的點以不同個數的圈選做出各種組合)

Dichotomy 指透過 Hypothesis 對所有 x (input data) 運算的結果, Dichotomies H(x₁, x₂, ... x_N) 表示這些不同 結果的集合, 集合內個數上限稱為 Effective Number of Lines。

Target

目標在於找到一個方法, 可以有效的將 ∞ 多個 Hypothesis 對應找到分類後的個數可以 << 2^N (大於 2^N 會讓 Top III 的不等式右項無法收斂), 而這個目標的關係式稱作 Growth Function

Growth Function m_H(N) = max | H(x₁, x₂, ... x_N) | ≤ 2^N

Break Point 第一個資料點 K 使得 m_H (K) < 2^K, 在 K < N 皆會成立 (K 不一定存在, 但如果有 K 存在, 這個演算法的錯誤率收斂似乎就相當有機會)。

Example

• Growth Function for Positive Rays (大於某個 threshold 結果為正), 則 ∞ 的 H 為 h(x) = sign( x - threshold ), 但 Growth Function 為 $m_{\mathcal{H}(N)}=N+1$, 因為僅有 N+1 種可以放置 threshold 的組合。

• Growth Function for Positive Intervals (在某個區間內時, 結果為正), 則 ∞ 的 H 為 h(x) = +1 if x ∈ [l, r), -1 otherwise, 但 Growth Function 為 $m_{\mathcal{H}(N)}=\binom{N+1}{2} + 1 = \frac{1}{2}N^2 + \frac{1}{2}N + 1$ (all -1 的 case)。

• Growth Function for Convex Sets (凸多邊形內的區域結果為正), 其中一種可能是將所有資料排成圓形, 並將結果為正的點連線成多邊形, 此時 2^N 所有種排列皆可以產生, 因為 Growth Function 是取 max, 所以僅需要造出這組, 即可得知 Growth Function 為 $m_{\mathcal{H}(N)}=2^N$。

  這個當任意挑選 N 個 input 卻有可能造出 2^N 個所有 output 排列組合的 case 稱作 Shattered。

Conjecture 猜想

• No break point: m_H(K) = 2^N (Shattered)
• Exist break point K: m_H(K) = O(N^K-1) 之後會證明

Proof

令 B(N,K) 為 Bounding Function, 其值是要抽象於 Growth Function 外只在乎其 Dichotomies 上限 (因為我們不一定知道手上 Hypothesis Set 的 Growth Function, 但想知道在 Break Point 存在的條件下, 是否可以侷限住 Hypothesis 的種類上限), 解讀為 N 個 input 中任意取 K 項的 Dichotomy 上限個數 (當 K 為 break point 時), 而這邊重點又在於已知任取 K 項時不會 Shattered (種類 < 2^K), 欲找出 B(N,K) ≤ 多項式的複雜度 (個數)。

B(N,K) = 2α + β (將 Bounding Function 裡的組合, 拆分為 α 表示 Dichotomy 中僅最末項不同的個數, β 是剩餘個數 兩種)

α + β ≤ B(N-1,K) (為去掉最末項後 僅 留下不同的 Dichotomy 個數, 因為 B(N,K) 告訴我們任 K 項不 Shattered, 所以只要 N-1 >= K 時 (下圖橘色標記部分), 剩下的項本身也不會 Shattered)

α ≤ B(N-1,K-1) (若任取 K-1 項會 Shattered = 2^K-1, 則加上之前去掉的最末項 = 2^K, 與 Bounding Function 定義衝突)

B(N,K) ≤ B(N-1,K) + B(N-1,K-1) (替換上式可得知)

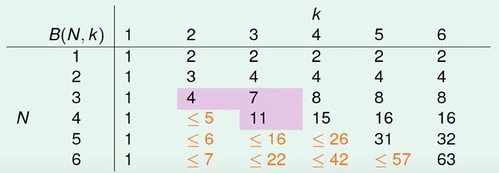
透過以上關係式, 可以用數學歸納法證明以下不等式, 而 RHS 的最高項為 N^k-1

$$\begin{equation} \begin{split} B(N,k)\leq \sum_{i=0}^{k-1}\binom {N}{i} \end{split} \end{equation}$$

當 N = 1 時代入很容易得知成立, 假設 N = N' 也成立, 透過以下推導得知 N = N'+1 也會成立, 得證 $$\begin{aligned} B(N'+1,k) &\leq B(N',k) + B(N',k-1) \\\ &\leq \sum_{i=0}^{k-1}\binom{N'}{i}+\sum_{i=0}^{k-2}\binom{N'}{i} \\\ &=1+\sum_{i=1}^{k-1}\binom{N'}{i}+\sum_{i=1}^{k-1}\binom{N'}{i-1} \\\ &=1+\sum_{i=1}^{k-1}[\binom{N'}{i}+\binom{N'}{i-1}] \\\ &=1+\sum_{i=1}^{k-1}\binom{N'+1}{i}=\sum_{i=0}^{k-1}\binom{N'+1}{i} \end{aligned}$$

所以得知, 當 Break Point 存在時, 其 m_H(K) 數量跟 N 的關係會是 polynomial N^k-1 (上式其實可以反向再證明 LHS = RHS, 不僅只是 upper bound), 而這個結果又讓我們知道當 Break Point 存在時, 挑選到錯誤的機率似乎是可以掌握的事。 $$\mathbb{P}_\mathcal{D}[BAD\ D]\leq 2\cdot2m_{\mathcal{H}}(2 \cdot N)\cdot exp(-2 \cdot \frac{1}{16} \epsilon ^2N)$$ 完整的不等式如上, 中間替換的過程需要一些數學上的技巧推導, 並非直接將 M 以 $m_{\mathcal{H}}$ 取代, 下一節將繼續證明這個不等式。