VC Dimension

VC Dimension ($V_{dc}$) = 'minimum K' -1

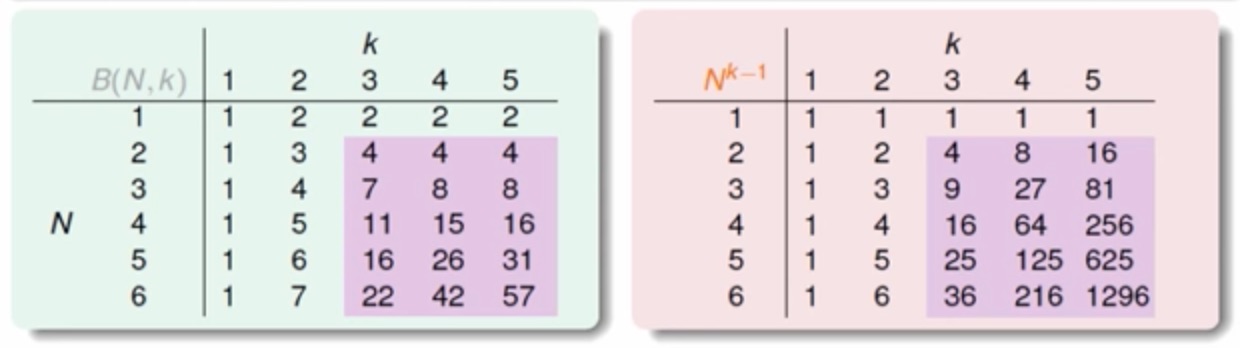$$\begin{aligned} \\m_{\mathcal{H}}(N)\leq \sum_{i=0}^{d_{vc}}\binom {N}{i}\leq N^{d_{vc}} \\\ \textit{( for }N\geq 2, d_{vc}\geq 2\textit{ )} \end{aligned}$$ 透過上圖可以簡化我們的式子 $$\begin{aligned} &\;\;\;\,\mathbb{P}[|E_{in}(g) - E_{out}(g)\gt \epsilon|] \\\ &\leq \mathbb{P}[BAD]\\\ &= \mathbb{P}[\exists h \in \mathcal{H}\text{ s.t. } |E_{in}(h)-E_{out}(h)|\gt \epsilon] \\\ &\leq 4m_{\mathcal{H}}(2N)exp(-\frac{1}{8}\epsilon^2N) \\\ &\leq 4(2N)^{d_{vc}}exp(-\frac{1}{8}\epsilon^2N) \\\ &\textit{( if }d_{vc}\textit{ is finite = k is exists)} \end{aligned}$$

機器學習的條件

• Good Hypothesis Set (有 Break Point)
• Good Data (N 夠大)
• Good Algorithm (可以挑到夠小 $E_{in}$ 的 Hypothesis)
• Good Luck

VC Dimension for d-D Perceptron

• 1-D perceptron: $d{vc} = 2$
• 2-D perceptron: $d{vc} = 3$
• d-D perceptron: $d{vc} =^? d + 1$

Proof

Step 1. 證明 $d_{vc} \ge d+1$

證明的方式就是要證明當 x 為 d 維度時, d + 1 個 output 可以被 shattered

設計一個特殊矩陣, 表示將 d+1 個 input 組成一個 X 矩陣 (X 反矩陣存在 invertible) $$X = \left[ \begin{matrix} - x_1^T - \\ - x_2^T - \\ - x_3^T - \\ : \\ - x_{d+1}^T - \end{matrix} \right] = \left[ \begin{matrix} 1&0&0&...&0 \\ 1&1&0&...&0 \\ 1&0&1&...&0 \\ &&:&& \\ 1&0&0&...&1 \\ \end{matrix} \right]$$ 根據定義

For any y, sign (Xw) = y, 那我們試著找一個 w 使得 Xw = y (假設存在這麼剛好的 X)

由前提知設計出的X 反矩陣存在, 所以 w = X^-1y 也會存在, 得證存在某個 hypothesis w 使得任意 y 都可以被產生出來 (Shattered)。

Step 2. 證明 $d_{vc} \le d+1$

證明的方式就是要證明當 x 為 d 維度時, d + 2 個以上的 output 都不能被 shattered

將之前設計的矩陣加入第 d+2 筆的 input $$X = \left[ \begin{matrix} - x_1^T - \\ - x_2^T - \\ - x_3^T - \\ : \\ - x_{d+1}^T - \\ - x_{d+2}^T - \end{matrix} \right]$$ 則 因為線性相依的關係 (d+1 維, 且 前 d+1 筆資料是線性獨立, 第 d+2 筆肯定能由前 d+1 筆向量組合而成)

$x_{d+2} = a_1x_1 + a_2x_2 + ... + a_{d+1}x_{d+1}$

假設 d+2 種 output 都能被 shattered 的話, 那麼 d+1 種的 output 也要能被 shattered, 所以此時我們假設存在 w 可以使得 $sign(a_n) = sign(w^Tx_n)$, 因為與係數同向也僅是其中一種 output y (Shatter 理應要存在)

$w^Tx_{d+2} = a_1w^Tx_1 + a_2w^Tx_2 + ... + a_{d+1}w^Tx_{d+1} \gt 0$ (恆成立)

所以至少有一種是無法被產生出來的 output, 那就是以上的 case 搭配上 $y_{d+2}$ < 0 (反證法得證)。

Degrees of Freedom (自由度)

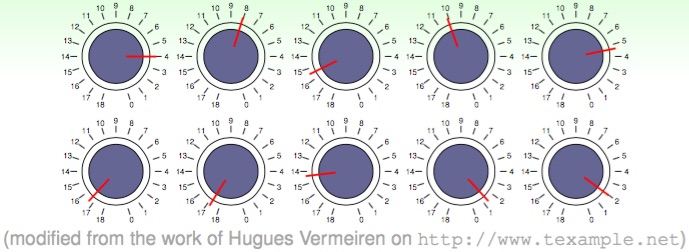VC dimension 代表的意思是 Hypothesis Set 裡的自由度, 雖然上面這些可控制的旋鈕 (假設是類比) 有無限多種組合, 但 $D_{vc}$ 是著眼真正有效的 (Effective Number of Lines) 種類有多少 (意涵對相同 input 可產生出不同結果)。

複雜度評估

$$\begin{aligned} \mathbb{P}[BAD] &= \mathbb{P}[\exists h \in \mathcal{H}\text{ s.t. } |E_{in}(h)-E_{out}(h)|\gt \epsilon] \\\ &\leq 4(2N)^{d_{vc}}exp(-\frac{1}{8}\epsilon^2N) \end{aligned}$$ 將右式定義為 $\delta$, 移項可得 $\epsilon = \sqrt{\frac{8}{N}ln(\frac{4(2N)^{d_{vc}}}{\delta})}$

$E_{in}(g)-\sqrt{\frac{8}{N}ln(\frac{4(2N)^{d_{vc}}}{\delta})} \leq E_{out}(g) \leq E_{in}(g)+\sqrt{\frac{8}{N}ln(\frac{4(2N)^{d_{vc}}}{\delta})}$

重新定義 $\Omega (N,\mathcal{H},\delta) = 上式的\ \sqrt{...}\ 項$, 稱作 Penalty for Model Complexity (Model 是指 hypothesis, 而這個 penalty 就是指在我們要有多強的 Hypothesis Set 時, 所需付出的代價)

筆者按：筆者的理解, 是說今天這個不等式觀察的角度如果將重心放中, 目標希望 $\delta$ 發生壞事情的機率降低到某個門檻, 此時 Learning Model 的 $E_{in}$ 與 $E_{out}$ 的距離關係。(只是將不等式鎖定的變量代換而已)

• $d_{vc} \uparrow: E_{in} \downarrow but\ \Omega\uparrow$
• $d_{vc} \downarrow: E_{in} \uparrow but\ \Omega\downarrow$
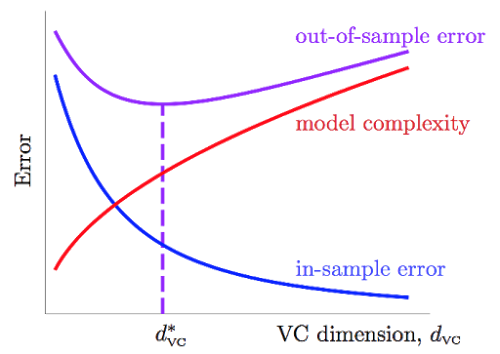
• best $d^*_{vc} in the middle$

透過上式可以了解, 並非一昧地追求 VC dimesion 愈大愈好, 而另一個使用 VC bound 的方式, 是用來侷限資料量 稱 Sample Complexity, 當今天目標鎖定了 $\epsilon, \delta, d_{vc}$ 我們究竟需要多少的 input 才能達到符合 $\lt \delta$ 的目標。

$\epsilon = 0.1$, $\delta = 0.1,$ $d_{vc} = 3$, 迭代不同的 $d_{vc}$ 所求出的關係式 $N\approx 10,000d_{vc}$

但是通常 $N\approx 10d_{vc}$ 實務上已足夠。(也隱含著 VC Bound 實際上是相當寬鬆不精準的上限)

Summary

目前透過數學工具的推導, 我們了解到了兩件事情

第一件事

Linearly Separable Data

$\downarrow$

PLA can converge (推導出 $cos\theta$ 與 迭代次數 $\sqrt{T}$ 成正比)

$\downarrow$ if T enough large

$E_{in}(g) = 0$

第二件事

with x_n ~ P and y_n = f (x_n)

$\downarrow$

$\mathbb{P}[|E_{in}(g) - E_{out}(g)\gt \epsilon|] \le ...$ by $d_{vc}$ is finite (此章節推廣至 d-D perceptron 也成立)

$\downarrow$ if N enough large

$E_{in}(g) \approx E_{out}(g)$

綜合以上兩件事

$E_{out}(g) \approx 0$

Homework 補充

證明參考

$d_{vc}(\cup_{k=1}^{K}\mathcal{H}_k) = d_{vc}(\mathcal{H}_1)+d_{vc}(\mathcal{H}_2)+ K - 1$